
#ARITHMETIC AND GEOMETRIC SEQUENCES FORMULAS SUM SERIES#
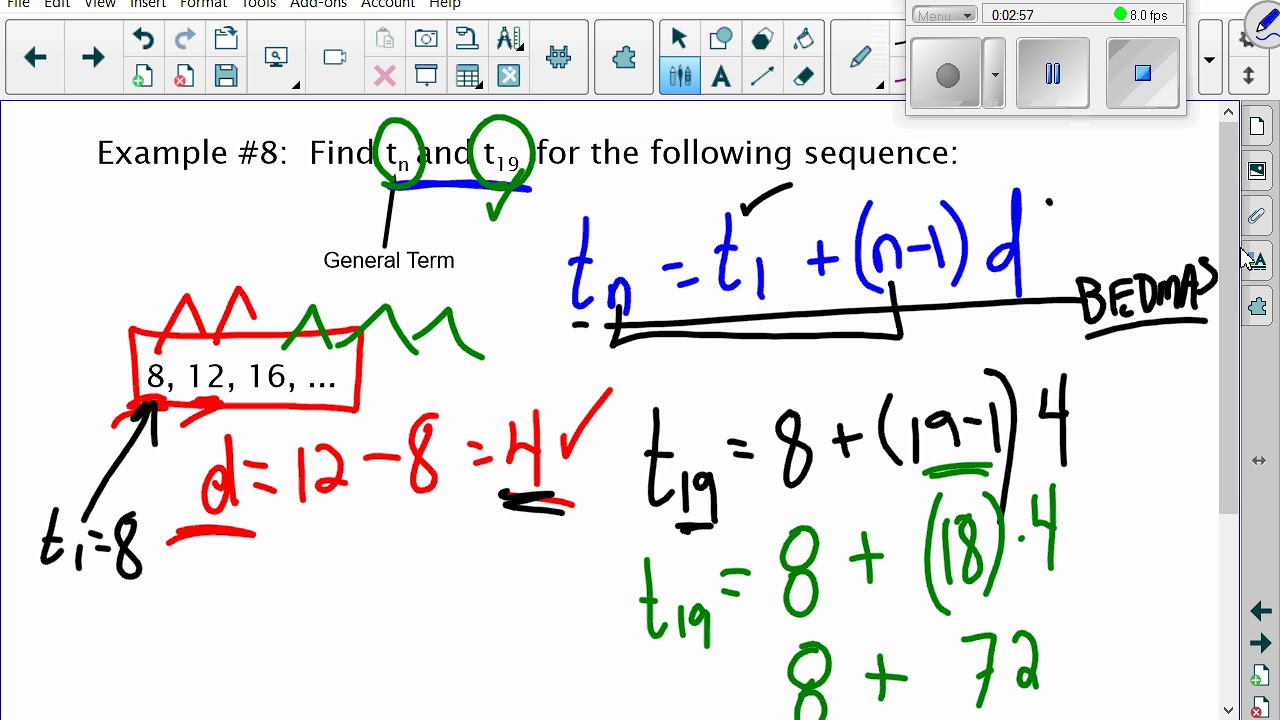
We start by using the Arithmetic Series formula to find the sum of various Arithmetic Series, and then we will work backwards, from our Sum and locate the first term and the common difference. Specifically, you might find the formulas an a + (n 1)d (arithmetic) and an a rn 1 (geometric).
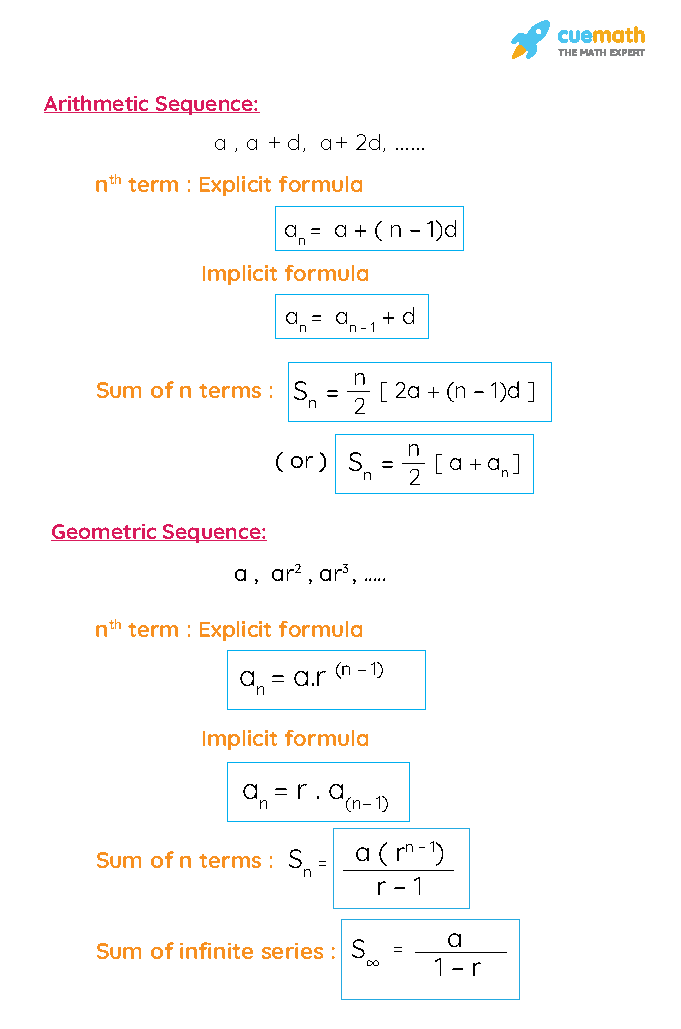
What is extremely important to note, and should be a warning to us, is that we can only find the sum of an Arithmetic Series that is Finite! That means, we can only find the sum for the first n terms. If you look at other textbooks or online, you might find that their closed formulas for arithmetic and geometric sequences differ from ours. a formula for the sum of the first n terms of a geometric sequence, . EXAMPLE 1 Use the partial sum formula to find the sum of the first six terms of the arithmetic sequence 2, 5, 8, 11, 14, 17, c. We will begin by exploring the Arithmetic Series and it’s Summation Formula. Similar to an arithmetic sequence, a geometric sequence is determined completely. Thus making both of these sequences easy to use, and allowing us to generate a formula that will enable us to find the sum in just a few simple steps. Use the following formula to find any term of an arithmetic. So the next three terms are 17, 21, and 25. Then add 4 to 17 to get the next term to get 21, etc. To get the next three terms, add 4 to 13 which equals 17, the next term in the sequence. Now, remember, and Arithmetic Sequence is one where each term is found by adding a common value to each term and a Geometric Sequence is found by multiplying a fixed number to each term. Arithmetic Sequences Arithmetic sequences are sequences with a common di erence, that is to say, that the di erence between consecutive terms is constant. 1, 5, 9, 13, I can see that this is an arithmetic sequence with a common difference of 4. Well, happy day! Because this lesson is all about two very special types of Series: Arithmetic and Geometric Series where all we have to do to is plug into a formula! The difference between the two types of sequences is that in arithmetic sequences the consecutive numbers in a set differ by a fixed amount known as the common. An infinite geometric series converges (has a sum). Jenn, Founder Calcworkshop ®, 15+ Years Experience (Licensed & Certified Teacher)īut wouldn’t it be nice if we didn’t have to add up all those terms? If only there was a formula that we could just plug into! When 1 < r < 1 you can use the formula S a 1 1 r to find the sum of the infinite geometric series.


 0 kommentar(er)
0 kommentar(er)
